この記事では「力学的エネルギー保存の法則」について中学生向けに解説を行います。
- 力学的エネルギー
- 運動エネルギー
- 位置エネルギー
について知りたい方は、この記事を読めばバッチリです。
 ねこ吉
ねこ吉よろしくお願いします!
うん。よろしくね!
自己紹介
「さわにい」といいます。元中学理科の教員。
現在は毎月30万人が利用する理科サイトの運営者です。
登録者9万の教育YouTuberでもあります。
さわにいと理科の成績を上げる塾「さわにい理科塾」やってます!
それでは解説スタート!
運動エネルギーとは
さて、「力学的エネルギー」について解説していきたいんだけど、それにはまず「運動エネルギー」と「位置エネルギー」について説明する必要があるんだ。



運動エネルギーと位置エネルギー?
うん。運動エネルギーと位置エネルギーがわからないと、力学的エネルギーの説明をすることができないんだ。
だからまずは、運動エネルギーについて解説していくね!



わかりました。お願いします!
運動エネルギーとは、運動している物体がもつエネルギーのことなんだよ。
- 運動エネルギーとは
- 運動している物体がもつエネルギーのこと



運動している物体?
うん。理科では「動いている」ということを「運動している」ともいうんだよ。
だから運動エネルギーは「動いている物体がもつエネルギーのこと」とも言えるね!
例えば動いている野球ボールが体に当たると痛いよね。
これは、動いている野球ボールが、運動エネルギーをもつからなんだね。





動いている物体は、運動エネルギーをもつんだね!
次に、運動エネルギーの大きさの変化を詳しくみてみよう。
運動エネルギーと物体の速さ
運動エネルギーは物体の速さが大きいほど、大きくなるよ。
ポイント
物体の速さが大きいほど、運動エネルギーは大きい。
これを図にすると、下のようになるね。
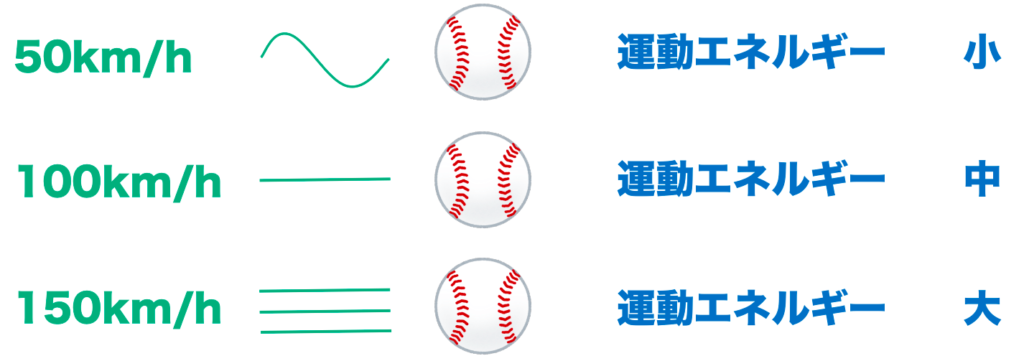

同じ野球ボールでも、速さが大きほど当たった時に痛いよね。
これは、速さが大きいほど運動エネルギーが大きくなるからなんだよ。



速さが大きいほど、運動エネルギーは大きい!
運動エネルギーと質量
運動エネルギーの大きさは、速さ以外に「質量」も関係があるんだよ。
(質量とは、簡単に言うと「重さ」のことだね。)
下の図を見てみよう。
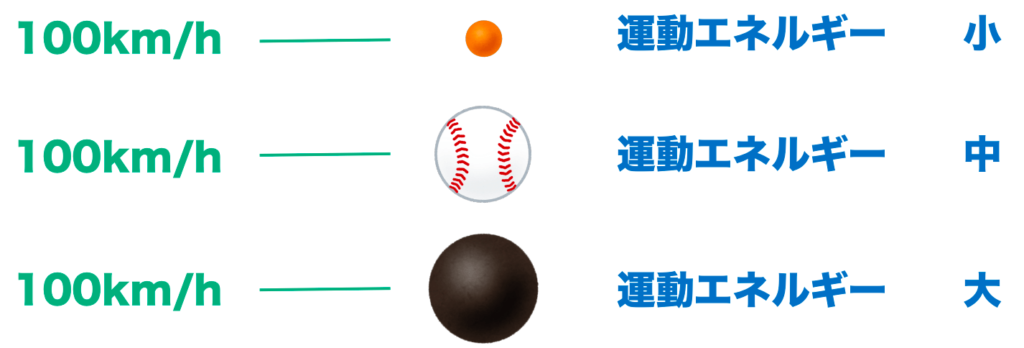

どうかな?同じ100km/hの速さでも、ピンポン玉が当たるか、野球ボールがあたるか、鉄球が当たるかで、痛さは全然違うよね!



鉄球が当たったら大変!
本当だね。このように運動エネルギーは、物体の質量によっても変化するんだ。
同じスピードでも、質量が大きいほど運動エネルギーは大きいんだね。
まとめるよ
- 運動エネルギーとは
- 運動する物体がもつエネルギーのこと
運動エネルギーは
- 速さが大きいほど大きい
- 質量が大きいほど大きい
ということだね。しっかりと覚えておこう!



了解です!
位置エネルギーとは
次は「位置エネルギー」について説明していくよ。



力学的エネルギーの説明には、運動エネルギーと位置エネルギーを理解することが必要なんだよね。
そうそう。あまり難しくないから、しっかりとついてきてね!
位置エネルギーとは、高い位置にある物体がもつエネルギーのことなんだよ。
- 位置エネルギーとは
- 高い位置にある物体がもつエネルギーのこと



高い位置にある物体?
うん。例えば、止まっている鉄球でも、下の図のようにされたら怖いよね?





鉄球がぶら下がっているの?怖い!
そうだよね。つまり高い位置にあると(止まっていても)エネルギーをもつんだね。
そのエネルギーを「位置エネルギー」というんだよ!
位置エネルギーと物体の高さ
位置エネルギーは物体の高さが高いほど、大きくなるよ。
ポイント
物体の高さが高いほど、位置エネルギーは大きい。
これを図にすると、下のようになるね。


同じ野球ボールでも、高い位置にある方が、落とした時に足に当たると痛いよね。
これは、高い位置にあるほど位置エネルギーが大きくなるからなんだよ。



位置が高いほど、位置エネルギーは大きい!
位置エネルギーと質量
位置エネルギーの大きさは、高さ以外に「質量」も関係があるんだよ。
下の図を見てみよう。


どうかな?同じ高さでも、ピンポン玉が当たるか、野球ボールがあたるか、鉄球が当たるかで、落として足に当たったときの痛さは全然違うよね!



鉄球が当たったら痛すぎ!
本当だね。このように位置エネルギーは、物体の質量によっても変化するんだ。
同じ高さでも、質量が大きいほど位置エネルギーは大きいんだね。
まとめるよ
- 位置エネルギーとは
- 高い位置にある物体がもつエネルギーのこと
位置エネルギーは
- 高さが高いほど大きい
- 質量が大きいほど大きい
ということだね。しっかりと覚えておこう!



了解です!
力学的エネルギーとは
では力学的エネルギーについて解説をしていこう。



お願いします!
力学的エネルギーとは「運動エネルギー」と「位置エネルギー」を合わせたもの(足したもの)のことなんだ。
「足したもの」のことを「和」ともいうね。
- 力学的エネルギーとは
- 運動エネルギーと位置エネルギーの和
例えば運動エネルギーが「10」、位置エネルギーが「20」の場合は、力学的エネルギーは「30」になるということだね。
(10 + 20 = 30)
ポイント
運動エネルギー + 位置エネルギー = 力学的エネルギー
ではいよいよ、力学的エネルギー保存の法則について解説していくね!



ようやくだ!
力学的エネルギー保存の法則
力学的エネルギー保存の法則とは、「摩擦や空気抵抗がなければ、力学的エネルギーはいつも一定に保たれる 」という法則なんだ。
- 力学的エネルギー保存の法則
- 摩擦や空気抵抗がなければ、力学的エネルギーはいつも一定に保たれる



なんだか難しい…。
そんなに難しく無いよ。図で確認してみよう。
斜面を下る物体の力学的エネルギー保存
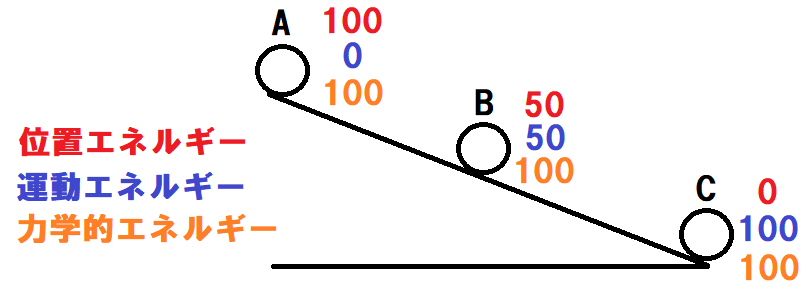

坂道を自然に下るボールで考えてみよう。(空気抵抗と摩擦は無視するよ)
- A地点ではボールは静止している
- A地点の位置エネルギーを100とする
として考えてみるよ。この場合、A地点では
- 運動エネルギー0
- 位置エネルギー100
- 力学的エネルギー100
となるね。
まだ静止している(止まっている)から運動エネルギーは0。位置エネルギーは初めに決めたように100。
力学的エネルギーは 0 + 100 = 100 だね。



うんうん。
続いてB地点でそれぞれのエネルギーを考えてみよう。


B地点ではボールが半分まで下ってきているね。
初めのころより、高さは小さくなっているけど、速さは大きくなっている状態だね。
つまりB地点でのそれぞれのエネルギーは
- 運動エネルギー50
- 位置エネルギー50
- 力学的エネルギー100
と考えることができるね。



位置エネルギーが小さくなったかわりに、運動エネルギーが大きくなったね。
そういうことだね。そして力学的エネルギーは 50 + 50 = 100だね。
最後にC地点を考えてみよう。


C地点では、最も低い位置にきているから、位置エネルギーは0になるね。
その反面、スピードは最も速くなっているから、運動エネルギーは最大になるね。
つまりC地点でのそれぞれのエネルギーは
- 運動エネルギー 100
- 位置エネルギー 0
- 力学的エネルギー 100
となるね。



うんうん。なるほど。
ここで注目してほしいのが、A〜C地点での力学的エネルギーエネルギーの変化だよ。
力学的エネルギーは、A・B・C。すべての地点で100のまま変化していないね。


このように、摩擦や空気抵抗がなければ、力学的エネルギーは変化しないことを「力学的エネルギー保存の法則」というんだね。
今回のそれぞれのエネルギーの変化をグラフで見てみよう。
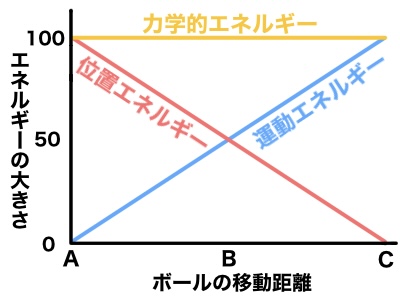

運動エネルギーはだんだん増加(スピードが上がる)
位置エネルギーはだんだん減少(高さが下がる)
力学的エネルギーは一定
となっているね。これが「力学的エネルギー保存の法則」だよ。



承知しました!
補足1
今回イメージしやすいように、それぞれのエネルギーを数字で表しました。
実際のエネルギーの計算方法は高校生で学習するよ!
補足2
摩擦や空気抵抗を無視しない場合は力学的エネルギーは保存されないよ。
ふりこの力学的エネルギー保存
続いてはふりこの力学的エネルギー保存を考えてみよう。
ふりことは、下の図のようなものだね。
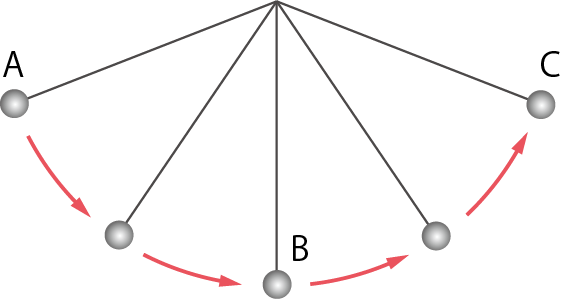

ポイント
摩擦と空気抵抗を無視すると、ふりこは永久に動き続けるよ!
まずはこのふりこの、A地点とC地点のエネルギーについて考えてみよう。
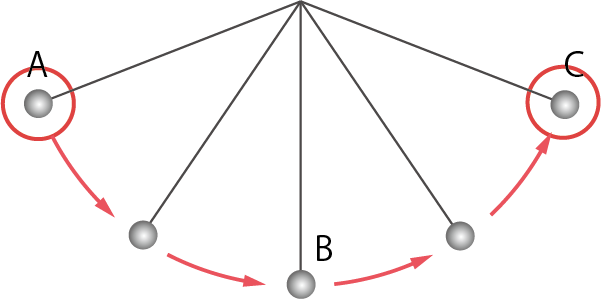

このふりこのA地点とC地点では、おもりが最も高い位置にきているね。
つまり、A地点とC地点では、ふりこのおもりの位置エネルギーが最大になっているんだ。
その反面、A地点とC地点では、おもりの動きが(一瞬)止まるね。つまり、運動エネルギーは0になるんだね。
- A地点とC地点では
- 位置エネルギーは最大
運動エネルギーは0
続いてB地点を見てみよう。
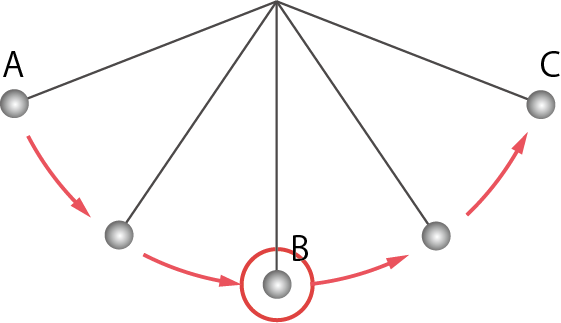

B地点では、このふりこの最も低い位置におもりがきているね。つまり地点では、位置エネルギーが最小(0)になっていると考えられるね。
反対に、おもりのスピードはB地点が最大になるよ。つまり運動エネルギーはB地点が最大だね。
- B地点では
- 位置エネルギーは0
運動エネルギーは最大
これをグラフにしてみると、下のようなグラフになるよ。
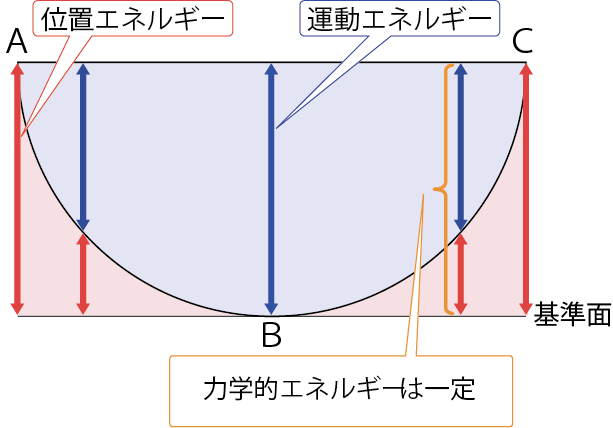

A地点・C地点では位置エネルギーが最大に、B地点では運動エネルギーが最大になっているね。
そして、運動エネルギーと位置エネルギーを合わせたもの、力学的エネルギーは一定になっているね。
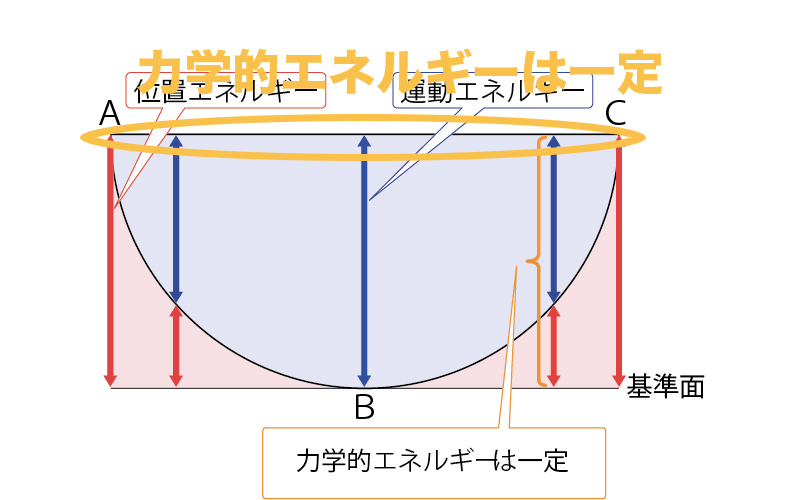

これがふり子のエネルギーの変化だよ。
力学的エネルギーのよくある問題
最後に力学的エネルギーのよくある問題を見てみよう。
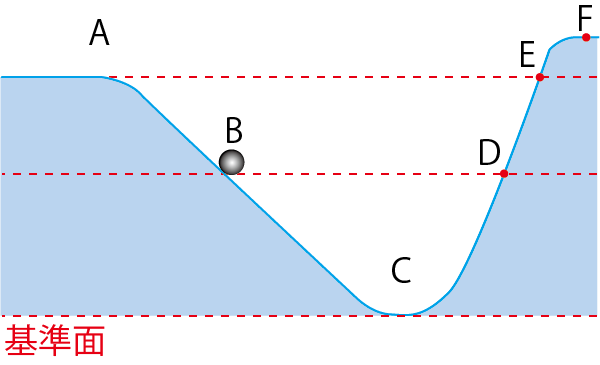

図のBの位置から静かに手を離した場合、鉄球はC~Fのどの位置まで上がるかな?
摩擦や空気抵抗を無視できるとして考えよう。



摩擦や空気抵抗が無視できるなら、Bと同じ高さのDまで上がるのかな?
素晴らしい!大正解だよ。摩擦や空気抵抗が無視できる場合は、力学的エネルギーが保存されるため、始めと同じ高さまで上がると覚えておこう。
Aからてを離せば、Eの高さまで上がるということだね。
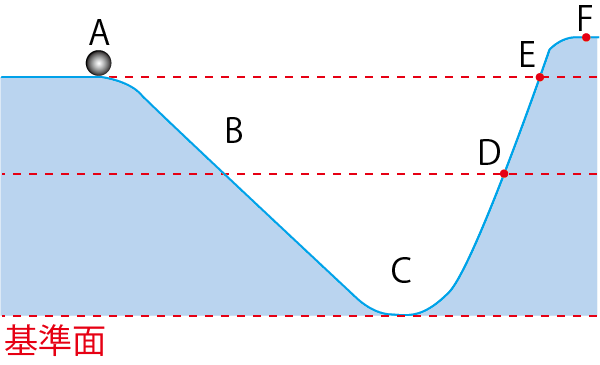

これで力学的エネルギー保存の法則の解説を終わるよ。
- 運動エネルギー
- 位置エネルギー
- 力学的エネルギー
という言葉をしっかりと確認しておこうね!



了解です!
他にも勉強したい内容がある場合は、トップページから探してみてね。
それではまたね!












コメント