このページでは、中学3年生で学習する「力の合成」について解説をしていきます。
- 一直線上の力の合成
- 角度のある力の合成
について知りたい方は、この記事を読めばバッチリですよ!
 ねこ吉
ねこ吉よろしくお願いします!
うん。よろしくね!
自己紹介
「さわにい」といいます。元中学理科の教員。
現在は毎月30万人が利用する理科サイトの運営者です。
登録者9万の教育YouTuberでもあります。
さわにいと理科の成績を上げる塾「さわにい理科塾」やってます!
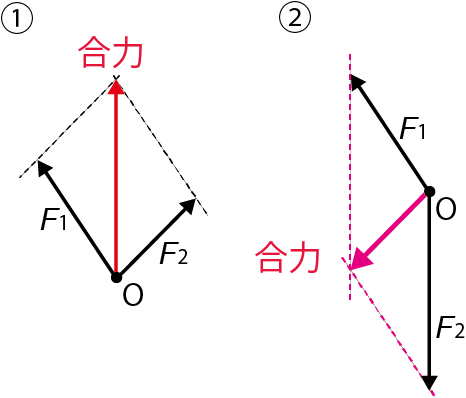
力の合成とは
力の合成とは、複数の力を合わせて1つの力とみなすことだよ。
また、合成してできた力のことを合力というよ。
下の図の赤色の矢印が合力だね。




力はどのように合成したらよいの?
力の合成の仕方には2つのパターンがあるんだ。
- 一直線上にはたらく2力の合成
- 角度をもってはたらく2力の合成
それぞれやり方が異なるんだ。
まずは、一直線上にはたらく2力の合成の仕方から解説をするね。
一直線上にはたらく2力の合成
では一直線上にある力の合成の解説をはじめよう。



一直線上にある力の合成?
うん。たとえば下の図①〜③のような力の合成だね。
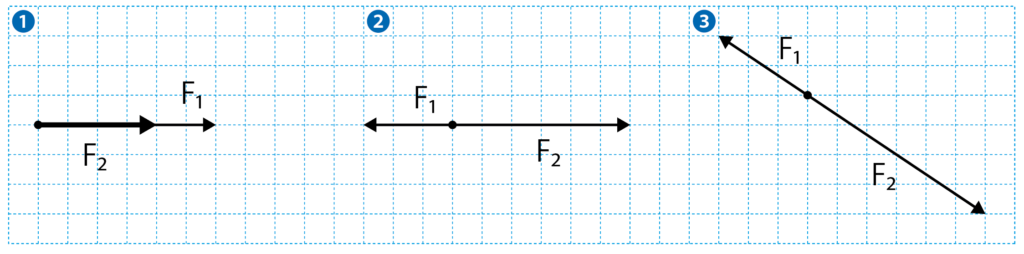

これら①〜③の力は、一直線上にはたらいているね。
一直線上ににはたらく力の合成の考え方は簡単。次の2つのポイントを守るだけだよ。
一直線上にはたらく力の合成
力の向きが同じであれば、たす。(+)
力の向きが反対であれば、ひく。(ー)
これだけなんだ。



足し算、引き算だけでいいの?
うん。そうなんだよ。
①を見てみよう。これはF1は右へ6マス分。F2は右へ4マス分の力だね。



力が同じ向きだから、足し算でよさそうだね。
そうだね。つまりこの2つの合力は、F1とF2の力を足した、右へ10マス分となるんだね!
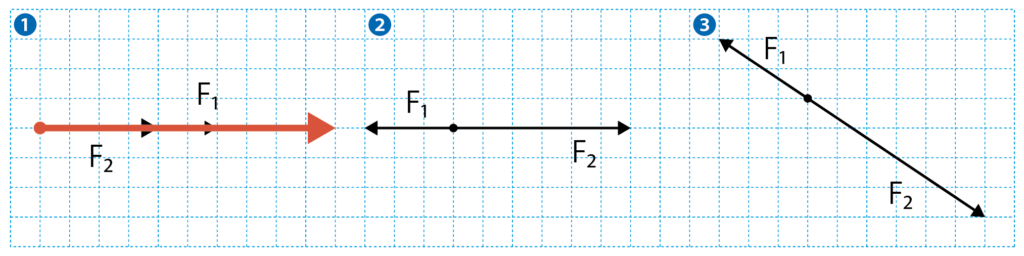

これだけだよ。とても簡単だから、必ずできるようにしようね!
②、③は、反対の向きだから、それぞれの力を引き算すればいいね。
すると、答えは次のようになるね。
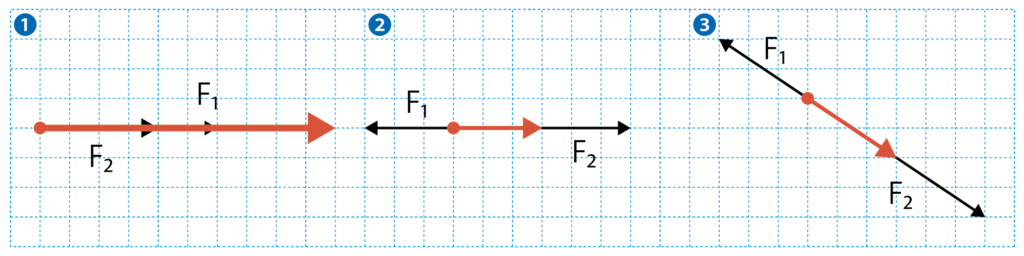

②は力が大きい、F2からF1の力を引いたものが合力だね。
同様に、③も力が大きい、F2からF1の力を引いたものが合力だね。



確かに矢印の足し算、引き算だけで答えが出せるね!
そうなんだ。
これが「一直線上にはたらく力の合成」だよ!
角度をもってはたらく2力の合成
では続いて「角度をもってはたらく力の合成」について考えていこう!
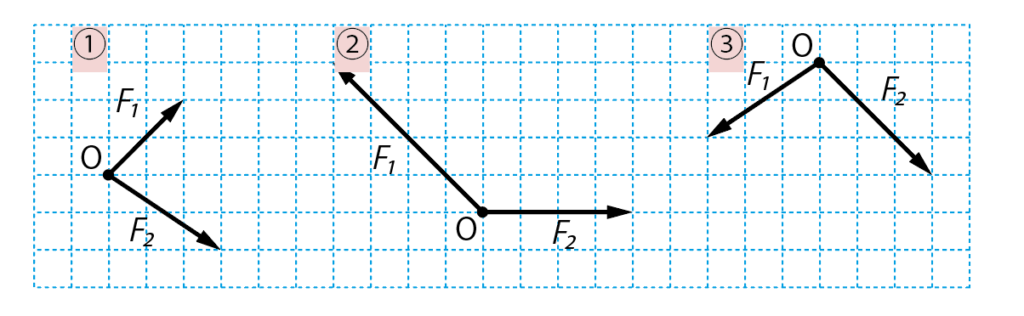

これらが角度をもってはたらく2力だね。



確かに角度がついているね?この場合の合成はどうするの?
このような場合は、2つの力を辺とする、平行四辺形を書けばいいんだよ。
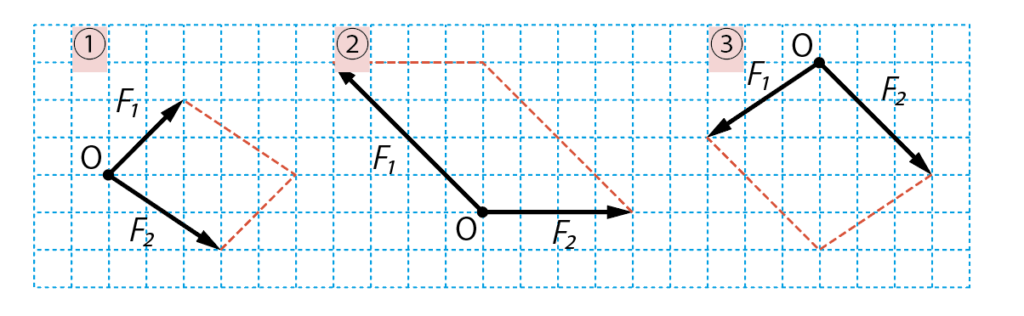

そして、平行四辺形の対角線に引いた矢印が、合力になるんだよ。
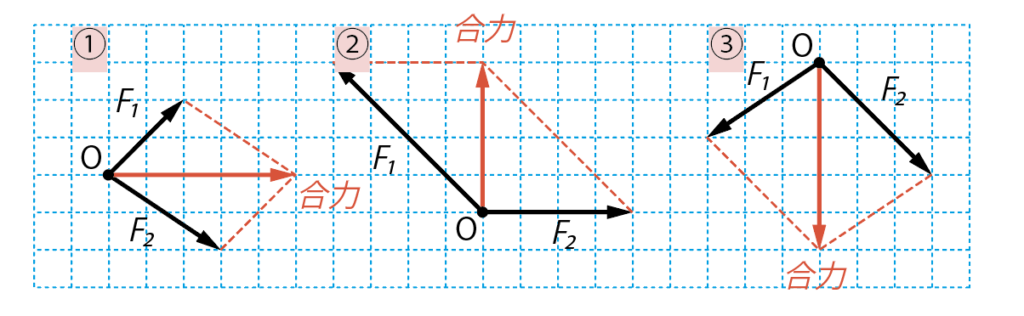

これが、角度をもってはたらく2力の合成の仕方だよ。
まとめ
これで力の合成に関する解説を終わるよ。
- 一直線上の力の合成
- 角度のある力の合成
それぞれ合成の仕方が異なるから、整理して覚えておこうね!
さわにいは、登録者9万人の教育YouTuberです。
中学の成績を上げたい人は、ぜひYouTubeも見てみてね!
また、さわにいと理科の成績を上げる塾「さわにい理科塾」もやってます!
他のページも見たい人はトップページへどうぞ。



またねー!












コメント