このページでは
- フックの法則とは何か
- 力の大きさとばねの関係
について中学生向けに解説をしています。
このページを読めば、ばねの問題はバッチリだよ!
自己紹介
「さわにい」といいます。元中学理科の教員。
現在は毎月30万人が利用する理科サイトの運営者です。
登録者9万の教育YouTuberでもあります。
さわにいと理科の成績を上げる塾「さわにい理科塾」やってます!
 ねこ吉
ねこ吉ねこ吉です。みんなよろしく!
ではフックの法則の学習スタート☆
フックの法則
フックの法則の解説を始めるね!
苦手な人も多いと思うけど、
一緒にがんばろう☆!
「フックの法則」とはこのようなものなんだ!
- フックの法則
- 力の大きさとばねののびは比例するという法則



これだけじゃ、よくわからないよ。
確かにわかりにくいね!
ねこ吉。「比例」ってどういうことかわかるかな?



それはわかるよ。片方が2倍になると、もう片方が2倍になるやつだよね。
そうそう。いいね。
つまりフックの法則とは、
力の大きさが2倍、3倍…となると、
ばねののびも2倍、3倍…。となる。
という法則なんだ。そんなに難しくないよ。
例を出しながら説明するね。
図1をみてみよう。


天井からばねが吊るさっているよ。
このとき、ばねはまったく伸びていないから、
ばねののびは0cmだね。
図2をみてみよう。


図1に質量100gのおもりを吊るしたよ。
ここで大切なのは、前のページで学習した、
100gの質量は、1Nの力(重力)
と考えられるということだね。
だから、ばねには1Nの力がはたらいているね。
図2をみると、
このばねを1Nの力で引っ張ると、ばねののびは2cm
となっているね。


図3をみてみよう。


図2からさらに100gおもりを追加して、
合計200g分のおもりを吊るしたよ。
質量が200gということは、力(重力は2N)だね。
つまり、ばねは2Nの力で引っ張られているね。
図3から、このばねを2Nの力で引っ張ると、ばねののびは4cmとわかるね。


図1~図3をまとめてみると、このようになるね。


これを表にしてみよう。


このようになるね。
ここで、力の大きさとばねののびの関係に注目しよう。
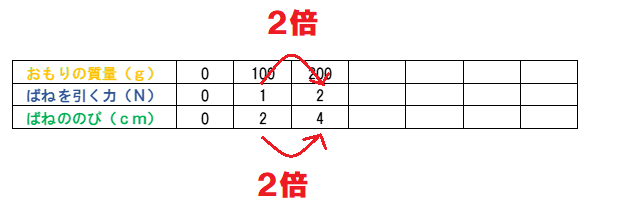

力の大きさが2倍になると、ばねののびも2倍となっているね。これは比例の関係だね。
これがフックの法則なんだ。



ほうほう。なるほど。
表に空欄があるけど、フックの法則を利用すれば、すべてうめることができるんだ。


このように、
力が3Nならばねののびは6cm
力が4Nならばねののびは8cm
という風に、比例の関係は続いているね。


これがフックの法則だよ。



計算だけでばねののびを予想出来て便利だね☆
ほんとだね!


さて、ここで注意事項だよ。
1Nの力で何cmばねが伸びるかは、やってみないとわからないよ。
ばねの種類によって、
- 「よくのびるばね」や、
- 「あまりのびないばね」
があるんだ。
例① やわらかいばね(よくのびるばね)の場合
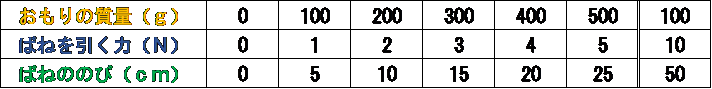
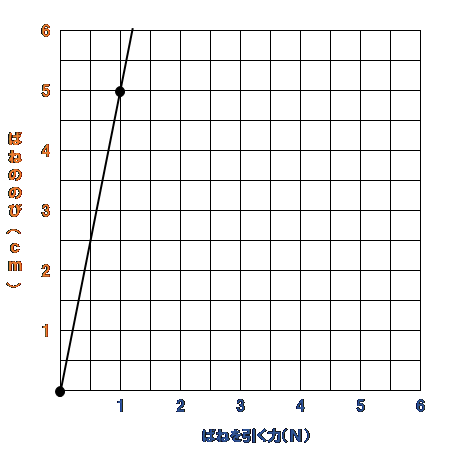
この例①のばねの場合は、1Nの力で、5cmもばねがのびているね。
このやわらかいばねの場合も、フックの法則が成り立って、力の大きさが2倍の2Nになると、ばねののびも2倍の10cmになっているね!
例② かたいばね(あまりのびないばね)の場合
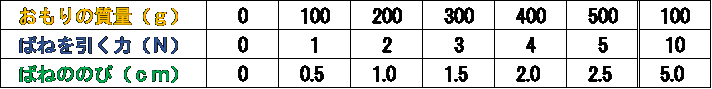
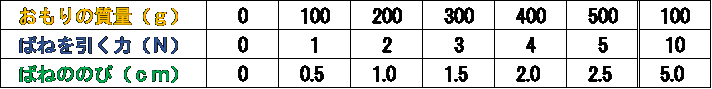
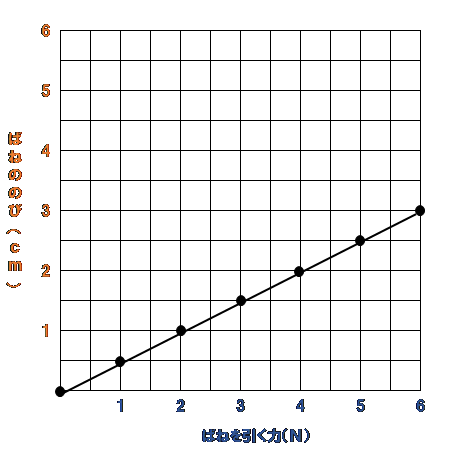
この例②のばねの場合は、1Nの力で、0.5cmしかばねがのびないね。
このかたいばねの場合も、フックの法則が成り立って、力の大きさが2倍の2Nになると、ばねののびも2倍の1.0cmになっているね!



1Nで何cmばねがのびるかは、ばねの種類によって違うんだね。
だけど、すべてのばねでフックの法則は成り立つんだね!
うん。その通りだよ。
もうひとつ注意事項だよ。
注意
テストでは、「ばねののび」ではなく「ばねの長さ」という書き方でひっかけ問題がでることがあるよ。
少し説明するね。
例題③ ばねの長さが5cmのばねに、質量100gのおもりを吊るしたら、ばねの長さは7cmになった。
このばねに質量200gのおもりを吊るしたら、ばねの長さは何cmになるか。
答え 9cm
なんでかわかるかな?
問題をよく読んでみよう。ここでのポイントは、「ばねののびが5cm」ではなくて、
「ばねの(もともとの)長さが5cm」というところだね。図で表すとこんな感じ。


このばねに、質量100gのおもりを吊るしたんだね。
質量100gは力になおすと、1Nだね!1Nの力が加わると、ばねの長さは7cmになった。


つまり、「最初の状態からばねは2cmのびているね!」ここがポイントなんだ!
そして、「質量200gのおもりを吊るすと、ばねの長さは何cmになるか。」
質量200gを力になおすと2Nになるから、ばねは最初の状態から4cmのびるはずだよね。
だから下のような図になるはず。


つまり、ばねの長さは9cmになるということだね!
(もともとのばねが5cmで、4cmのびたから 5+4=9)
このように、テストでは
「ばねののび」なのか
「ばねの(全体の)長さ」なのか、
いつも注意するようにするといいよ!
フックの法則とグラフ
フックの法則はグラフで出題されることもあるよ。
このページで学んだばねののびの表を、グラフにするとどのようになるか確認しておこう。
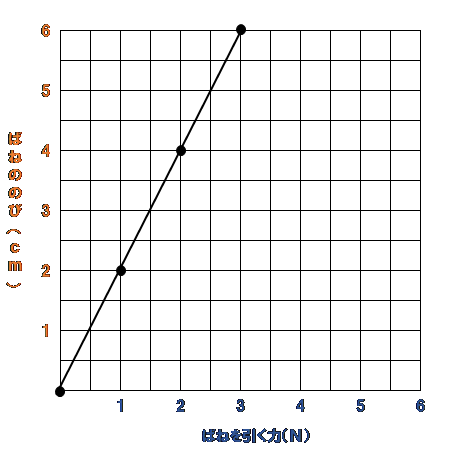
例①



例②
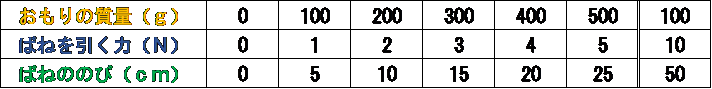
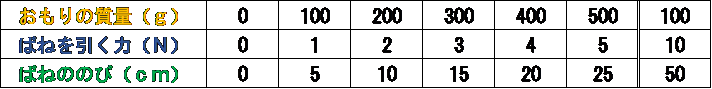

例③
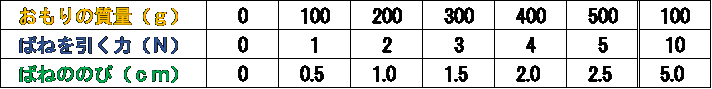

このような感じだね。
どれも比例のグラフだから、原点を通る直線のグラフになるね。
そして、よくのびるばねほど傾きが大きくなるんだね。
お疲れ様。これでフックの法則の説明を終わるよ。
応用問題も多いところだから、もっと勉強したい人は積極的に問題集にもチャレンジしてね。
ここで学んだ基本はどんな問題を解くのにも必要な考え方だから、また時間があるときに何回も読みにきてね!
続けて力の学習をしたい人は、下のボタンを使ってね!
①力のはたらき
②いろいろな力の種類
③力の単位、力と質量の関係
④フックの法則←今ここ
⑤力の矢印の書き方
⑥質量と重さの違い
⑦圧力とは何か、圧力の計算
⑧水圧
⑨浮力
⑩気圧
さわにいは、登録者9万人の教育YouTuberです。
中学の成績を上げたい人は、ぜひYouTubeも見てみてね!
また、さわにいと理科の成績を上げる塾「さわにい理科塾」もやってます!
他のページも見たい人はトップページへどうぞ。



またねー!












コメント
コメント一覧 (2件)
ばねの長さのグラフで、実際に実験してグラフを書くという課題が出たのですが、誤差があるため、直線がうまく引けません。中間の点を決めて書くと学校の教師が言っていたのですが、どうやって解くのかわかりません。ぜひ解説をお願いします。
具体的な問題がわからないので、正確なことは言えませんが、
リンク先のようなイメージで引いてみてください!(リンク先は電流のグラフですが、イメージはこんな感じです。)
https://www.google.com/url?sa=i&url=http%3A%2F%2Fphoto-m.tp.chiba-u.jp%2F~yjo%2Ftips%2Fgraph_howto.html&psig=AOvVaw0PeSGz9ADWf2xLQfrT4LVF&ust=1701900290170000&source=images&cd=vfe&opi=89978449&ved=0CBEQjRxqFwoTCLiL0uOm-YIDFQAAAAAdAAAAABAE