このページでは
- 抵抗の単位
- 抵抗のイメージ
- 直列回路の抵抗の計算
- 並列回路の抵抗の計算
を学ぶことができるよ!
また、このページは中二理科の
電気の単元の4ページ目なんだ。
全てのページを読むと電気の学習が完璧になるよ。
ぜひチャレンジしてみてね!
自己紹介
「さわにい」といいます。元中学理科の教員。
現在は毎月30万人が利用する理科サイトの運営者です。
登録者9万の教育YouTuberでもあります。
さわにいと理科の成績を上げる塾「さわにい理科塾」やってます!
このページの内容は、私が書いた下の本でさらにわかりやすく学習できます。
電気分解の苦手を無くしたい方は、よろしければご利用くださいね。
また、電気分野は動画でも解説をしています。動画が良い方は以下をご覧ください!
それでは抵抗の学習スタート!
抵抗の単位
では「抵抗の単位」の学習から始めるよ。
(前のページから読んできている人は流し読みでOKだよ。)
単位はとても簡単。「数字の後につけるもの」のことだよ。
例えば、
お金の単位は? → 円(日本では)
長さの単位は? → mm cm m km など
時間の単位は? → 秒 分 時間 日 年 など。
温度の単位は? → ℃ など
質量の単位は? → mg g kg など
面積の単位は? → cm2 m2 など
電流の単位は? → A mA など
こんな感じだね!
前のページから学習してきた人はもう大丈夫だね!
それでは、抵抗の単位の学習を始めよう!
抵抗の単位は「Ω」と書いて、「オーム」と読むんだよ!
だからテストで、「抵抗の大きさはいくつか」と聞かれたら
絶対に「○○Ω」と答えなければいけないんだね。
 ねこ吉
ねこ吉抵抗の問題が出た場合は、数字のあとに「Ω」をつけるんだね。
(ちなみに電流の単位は「A」電圧の単位は「V」だね。)
抵抗のイメージ
それでは抵抗の説明を始めるよ。まずはイメージづくりからだね。
「抵抗」とはその名前の通り、「電流の流れをじゃまする物」というイメージだね。
抵抗が大きいほど、流れる電流は小さくなるんだ。
下の図を見てね。
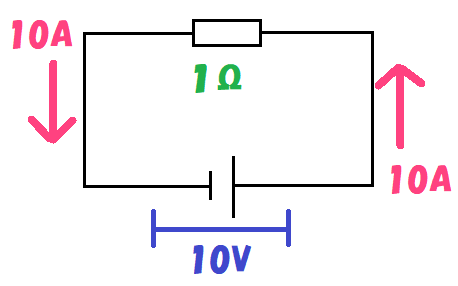



まず、電圧はどちらも同じ、10Vだね。
そして抵抗は、左の図が1Ω、右の図が2Ωだね。
右の図のほうが抵抗が大きいから、流れる電流が少ないね。
くり返すけど、
抵抗が大きいほど、流れる電流は小さくなるよ。
2つ注意を言うね。
①抵抗を通ると電流が減るわけではない


「電流」のページで勉強した人はOKだと思うけど、抵抗を通ると電流が減るわけではないよ。
上の図では、抵抗を通る前も後も、「10Aの電流」が流れているね。
抵抗が大きいと、「回路全体を流れる電流」が減るんだね。
もう一度図で確認してね!




2つ目の注意だよ。
②回路の問題では、抵抗と電球は同じと考えてよい。
回路には「電球![]()
![]()
この記号も、「抵抗![]()
![]()
「電球は光る抵抗」と考えるようにしよう!
直列回路の抵抗の計算
今から直列回路の抵抗の計算の説明をしていくよ。



直列回路の抵抗の計算?
そう。下の図のように回路に抵抗が直列に接続されている場合、回路全体の抵抗が何Ωになるかを計算できるようになってほしいんだ。
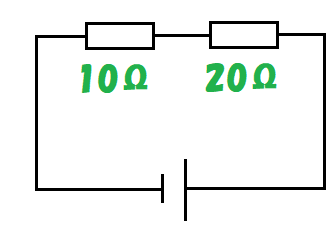

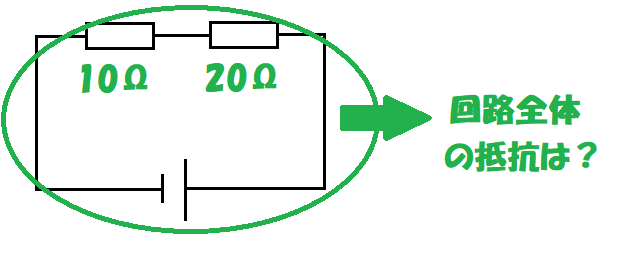

この回路全体の抵抗を計算できるようになろう!



はーい。
計算方法はとても簡単。抵抗をすべて足すだけだよ。


例えば上の回路図だったら、「10Ω」と「20Ω」が直列に接続されているから、
10+20=30 回路全体の抵抗は30Ωになるんだ。
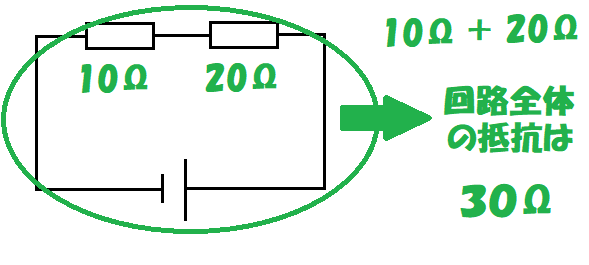




足すだけ?小学生でも出来そう…
ほんとだね。だけど
テストで出るとかなりの人が間違うんだよ。
難しい問題とかん違いするのかな?
みんなはしっかり勉強して、すらすら正解しよう☆
では例題をだすよ。
例1
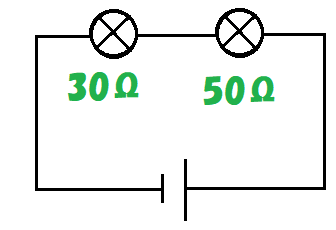
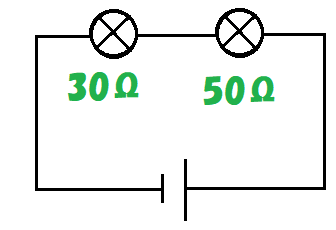
30Ωの抵抗の電球と、50Ωの抵抗の電球が直列に接続されているね。
回路全体の抵抗は何Ωかな?



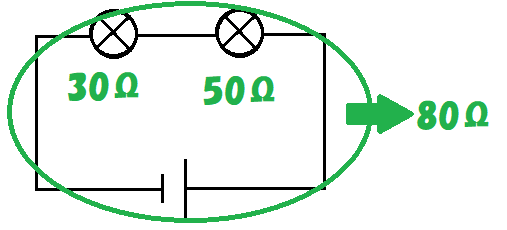
電球も抵抗と全く同じに考えていいから簡単だよ。30+50=80だね。
その通り。正解は80Ωだね。

例2
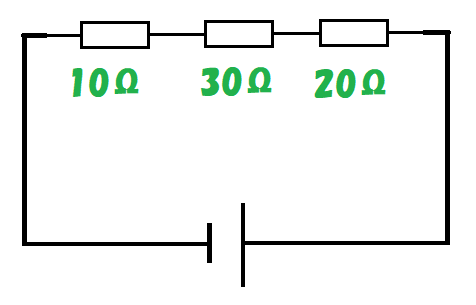

10Ωの抵抗、30Ωの抵抗、20Ωの抵抗が直列に接続されているね。
回路全体の抵抗は何Ωかな?
抵抗が3つになっても足し算するだけだよ。
10+30+20=60
答えは60Ωだね。
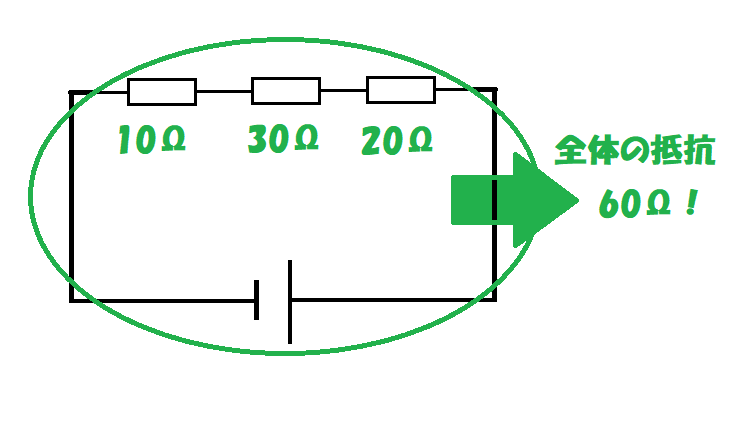

これを公式にしてみるよ。
抵抗の記号はRを使うから覚えておいてね。
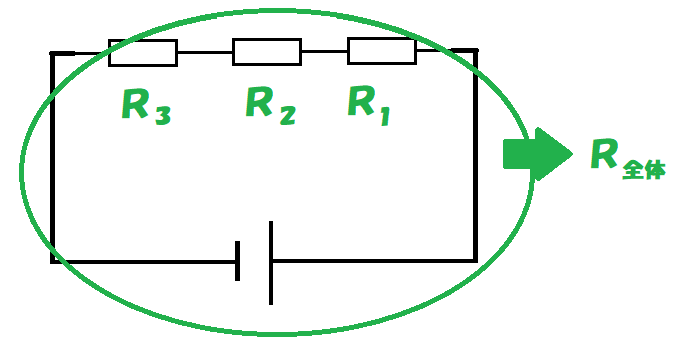

直列に接続された抵抗をR1、R2、R3とすると全体の抵抗R全体は
R全体=R1+R2+R3
となるんだ。
公式が苦手な人も
「直列に接続された抵抗は足すだけ」と覚えればいいんだよ☆
しっかりと覚えておこう!
並列回路の抵抗の計算
次に並列回路の抵抗の計算の説明をしていくよ。



並列回路だから「分かれ道がある回路」だね。
そうだね。
並列回路のほうが、公式や計算が難しいんだ。
だから気を付けて学習してね。
先に公式から説明するよ。
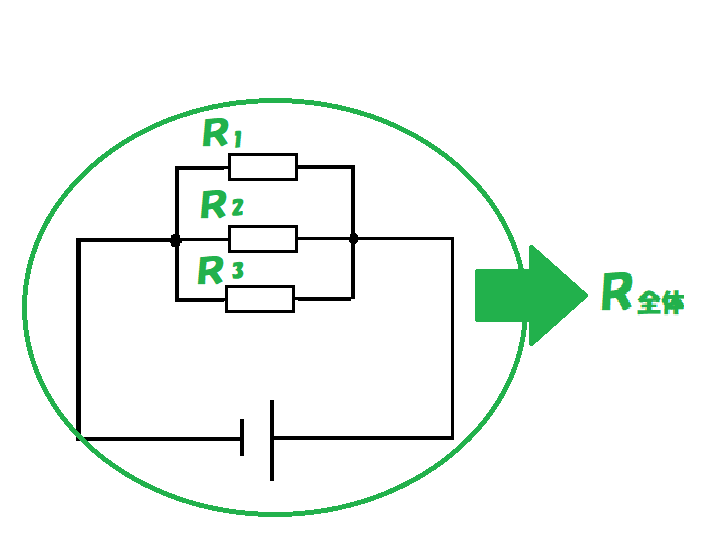

並列に接続された抵抗をR1、R2、R3とすると全体の抵抗R全体は
1 R全体 = 1 R1 + 1 R2 + 1 R3となるんだ。



たしかに覚えにくい…。
そうだよね。でも
「直列の公式の分子と分母がひっくり返った」
と覚えればわかりやすいかな?
計算も難しくなるから注意だよ。
それでは例題をやってみよう。
例1
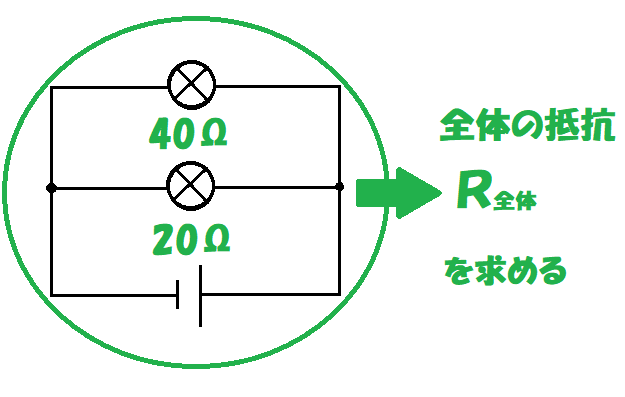

上のような回路があって、上の電球の抵抗は40Ω、下の電球の抵抗は20Ωだね。
回路全体の抵抗はいくつになるかな?
1 R全体 = 1 R1 + 1 R2 + 1 R3の公式にあてはめて考えてみよう!(今回はR3はいらないね)
1 R全体 = 1 40 + 1 20計算も難しいよ。まず通分をしよう
1 R全体 = 1 40 + 2 40右辺を足して
1 R全体 = 3 40ここで、方程式の左辺と右辺は、同時に分子と分母を逆にしてもいいというルールがあるから、両辺の分子と分母を入れ替えよう。
(このルールは覚えておくといいよ!)
R全体 1 = 40 3R全体=13.333回路
全体の抵抗は13.3Ω
が答えだね。(この問題ではとりあえず少数第一位まで出したよ。)



確かに、公式もだけど、計算もややこしい…。
ほんとだね。何回も練習してね。
おまけだけど
1 R全体 = 1 R1 + 1 R2 + 1 R3の公式が「覚えにくい」「計算が難しい」という人は
R全体 = R 1 × R 2 R 1 + R 2という公式もあるよ。
「分母は2つの抵抗を足す。分子は2つの抵抗をかける。」
と覚えればいいから楽だね。
計算も簡単だよ。
例1 をこの公式で解くと、


「分母は足す。分子はかける。だね」
R全体 = 40 × 20 40 + 20 R全体 = 800 60 R全体 = 80 6 R全体 = 40 3R全体=13.333
回路全体の抵抗は13.3Ω
となるね。



こっちの公式のほうがいいなー!
先生もいつもはこっちの公式で解いてるんだけど、1つ欠点があって…。
この公式は、抵抗が2つの時じゃないと使えないんだ。
抵抗が3つ以上あるときは、
1 R全体 = 1 R1 + 1 R2 + 1 R3こっちの公式を使わなければいけないんだ…。



そうなのか…。
両方覚えるか、初めのほうだけ覚えるかはみんなにまかせるね。
並列の抵抗の公式はみんな苦手なところだから、がんばるんだよ!
では例2にいくね。
例2
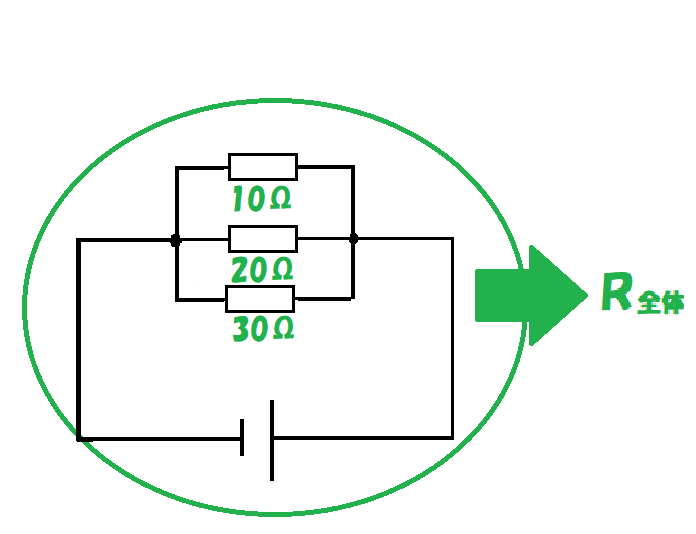

この10Ω、20Ω、30Ωの抵抗が並列に接続されているとき、回路全体の抵抗R全体は何Ωかな?
抵抗が3つだから、
1 R全体 = 1 R1 + 1 R2 + 1 R3の公式を使って解いていこう。
1 R全体 = 1 10 + 1 20 + 1 30通分して
1 R全体 = 6 60 + 3 60 + 2 60右辺を足し
1 R全体 = 11 60方程式の左辺と右辺は、同時に分子と分母を逆にしてもいいというルールがあるから、両辺の分子と分母を入れ替えよう。
R全体 1 = 60 11R全体=5.4545454545…
回路全体の抵抗は5.45Ω
が答えだね。(この問題ではとりあえず少数第二位まで出したよ。)
これで抵抗の計算の説明は終わりだよ。
問題集などで練習してみてね。
もう一度公式を確認しておくよ。
直列と並列で公式を混ぜないようにね!
直列回路の公式


R全体=R1+R2+R3
並列回路の公式


抵抗が2つのときは
R全体 = R 1 × R 2 R 1 + R 2でもOK☆
しっかりと覚えておこう!
導体と不導体
最後に導体と不導体の説明だけしておくね。
難しくないよ。
- 導体とは
- 電気を通しやすい物質のこと
主に金属などだね!
- 不導体(絶縁体)とは
- 電気を通しにくい物質のこと
主にゴム、ガラス、プラスチックなどだね。
不導体のことを絶縁体とも言うよ!
しっかりと覚えておこう!
これでこのページの勉強は終わりだよ。お疲れ様。
難しいところをよく頑張ったね!
次回は「オームの法則」を学習していくよ。
1ページ目から読んでいる人は、次のページを読めば回路の基本はOKになるよ☆
がんばろう!
みんなお疲れ様☆
続けて学習するには下のリンクを使ってね!
さわにいは、登録者9万人の教育YouTuberです。
中学の成績を上げたい人は、ぜひYouTubeも見てみてね!
また、さわにいと理科の成績を上げる塾「さわにい理科塾」もやってます!
他のページも見たい人はトップページへどうぞ。



またねー!












コメント
コメント一覧 (4件)
いーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーね!!!!!!!!
ありがとーーーーーーーーーございます!
とても参考になりました。
ありがとうございました。
お役に立ててよかったです!